Infrarot: Heizgesetze

Die Grundgesetze der Infrarotheizung

Mit der Entwicklung der IR-Erwärmung hat sich auch die grundlegende Wissenschaft, die die Funktionsweise der Wärmeübertragung unterstützt, weiterentwickelt. Es gelten jedoch drei Hauptgesetze:

• Stefan-Boltzmann-Gesetz: Gibt die Gesamtleistung an, die bei einer bestimmten Temperatur von einer IR-Quelle abgestrahlt wird.
• Plancksches Gesetz: Gibt die spektrale Verteilung der Strahlung einer Schwarzkörperquelle an, die bei einer bestimmten Temperatur 100% -Strahlung abgibt.
• Wiens Gesetz: In Anlehnung an das Plancksche Gesetz sagt dies die Wellenlänge voraus, bei der sich die spektrale Verteilung der von einem schwarzen Körper emittierten Strahlung an einem maximalen Punkt befindet.

Steffan-Boltzmann-Gesetz

Das Steffan-Boltzmann-Gesetz bezieht sich hauptsächlich auf das Infrarotemissionsvermögen. Berechnung der Leistungsstrahlung von einer IR-Quelle basierend auf der Oberflächentemperatur des Objekts und zusammen mit einem Schwarzkörperfaktor. Ein perfekter schwarzer Körper hat den Faktor 1 - wobei andere Materialien in diesem Faktor variieren (siehe Tabelle unten). Wenn wir das Emissionsvermögen normaler Materialien berücksichtigen, wird das Stefan-Boltzmann-Gesetz:

Nach dem Kirchhoffschen Wärmestrahlungsgesetz ist der Emissionsgrad für jeden beliebigen Körper, der Wärmestrahlung aussendet und absorbiert, gleich dem Absorptionsgrad. Das bedeutet, dass der Emissionsgrad nützlich ist, um zu bestimmen, wie viel eine Oberfläche absorbiert und emittiert.

Emissionsgradtabelle für verschiedene Oberflächen

Aluminium poliert 0.09	Messing poliert 0.03	Bronze poliertes 0.10
Kohlenstoff (Kerzenruß) 0.95	Keramik (glasiertes Porzellan) 0.92	Chrom poliertes 0.10
Konkreter 0.85	Kupfer poliert 0.02	Kupferoxidiertes 0.65
Quarzglas 0.75	Eisen poliert 0.21	Eisen verrostet 0.65
Kunststoff undurchsichtig 0.95	Silber poliert 0.05	Edelstahl poliert 0.16
Edelstahl oxidiert 0.83	Wasser 0.96

Mit diesem Gesetz können wir nun den Nettowärmeübergang zwischen zwei emittierenden Flächen bei T1 und T2 berechnen. Da beide emittieren, ist die Nettoleistungsübertragung die Differenz zwischen den beiden emittierten Leistungsausgaben.

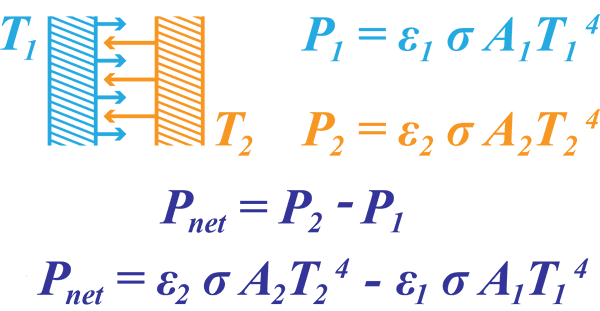
Plancksches Gesetz

Das Plancksche Gesetz beschreibt die elektromagnetische Strahlung, die von einem schwarzen Körper im thermischen Gleichgewicht bei einer bestimmten Temperatur emittiert wird. Es ist nach Max Planck benannt, einem deutschen Physiker, der es 1900 vorschlug.

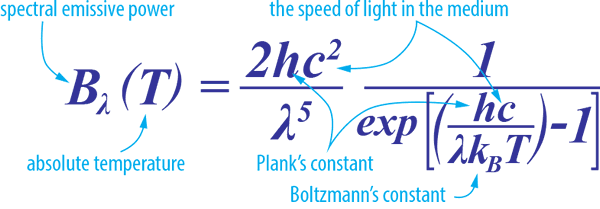
Wenn für verschiedene Heiztemperaturen (Emittertemperaturen) aufgetragen, sagt das Plancksche Gesetz Folgendes voraus:

1. Der Frequenzbereich, über den infrarote Heizenergie erzeugt wird
2. Die Emissionsleistung für eine gegebene Wellenlänge

Wir verweisen auf die unten stehenden Erläuterungen zum Planckschen Gesetz.

Wiens Vertreibungsgesetz

Das Wiensche Gesetz folgt dem Planckschen Gesetz und sagt die Wellenlänge voraus, bei der sich die spektrale Verteilung der von einem schwarzen Körper emittierten Strahlung am höchsten Punkt befindet.

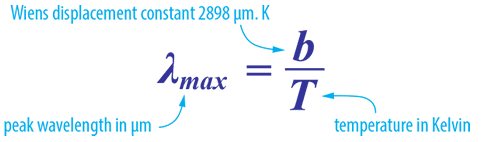
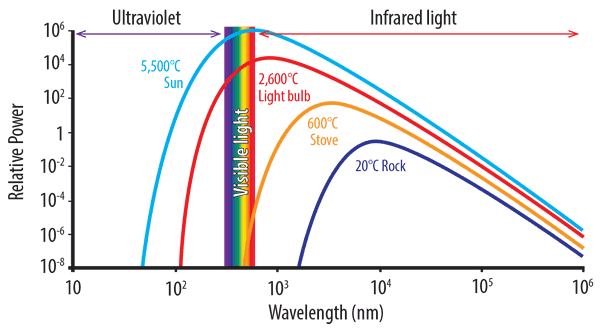
Ein perfekter Schwarzkörper ist eine Oberfläche, die nichts reflektiert und reine Wärmestrahlung abgibt. Der Graph von Leistung gegen Wellenlänge für einen perfekten Schwarzkörper wird als Schwarzkörperspektrum bezeichnet (siehe Abbildung unten). Beachten Sie die gepunktete rote Linie, die entsteht, wenn wir die Maximalpunkte jeder Temperaturkurve in der Planck-Verteilung verbinden und verbinden.

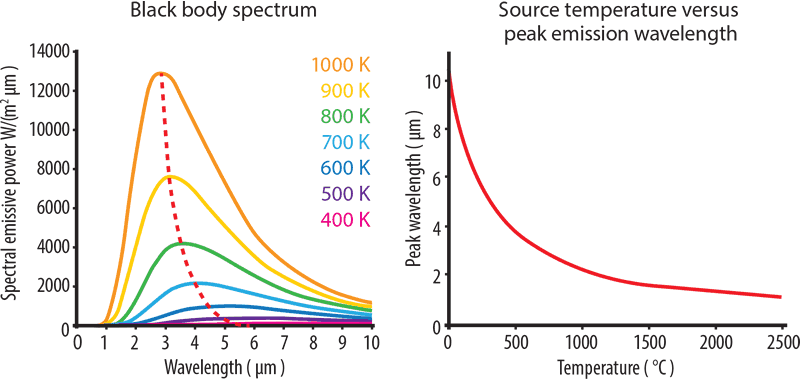
Mit steigender Temperatur erzeugt Wärmestrahlung Licht mit kürzerer Wellenlänge und höherer Energie. In der folgenden Grafik können wir sehen, wie eine Glühbirne eine bestimmte Energiemenge mit nur einem kleinen Teil im sichtbaren Spektrum erzeugt. Je höher die Temperatur und je kürzer die Spitzenwellenlänge, desto mehr Energie wird abgestrahlt.

Die Grafik zeigt auch, dass ein Gestein bei Raumtemperatur nicht „glüht“, da die Kurve für 20 ° C nicht in das sichtbare Spektrum hineinreicht. Wenn sich Objekte erwärmen, geben sie sichtbares Licht ab oder leuchten. Bei 600 ° C leuchten Objekte matt rot. Bei 1,000 ° C ist die Farbe gelb-orange und bei 1,500 ° C weiß.

Zwei weitere wissenschaftliche Gesetze bestimmen die praktische Anwendung von Infrarot-Strahlungswärme - die Inverse Square Law und Lamberts Kosinusgesetz.

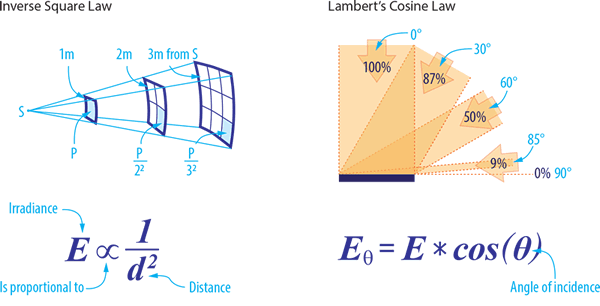
Inverse Square Law

Das Gesetz des umgekehrten Quadrats definiert das Verhältnis der Strahlungsenergie zwischen einer IR-Quelle und ihrem Objekt - dass die Intensität pro Flächeneinheit umgekehrt proportional zum Quadrat dieser Entfernung variiert. In der Praxis ist das Inverse-Square-Gesetz jedoch weniger effektiv, wenn es um große parallele Oberflächen wie beheizte Platten und Ofensysteme geht.

Lamberts Kosinusgesetz

Das Lambertsche Kosinusgesetz ermöglicht die Berechnung der IR-Intensität, wenn die Strahlung nicht direkt auf den Zielkörper angewendet wird, sondern in einem Winkel eingestellt ist. Dieses Gesetz gilt hauptsächlich für kleine Quellen, die über eine relativ große Entfernung strahlen.

Infrarotstrahler, die in der industriellen Erwärmung verwendet werden, haben im Allgemeinen eine verwendbare Spitzenemissionswellenlänge im Bereich von 0.75 bis 10 μm. Innerhalb dieses Bereichs gibt es drei Unterabteilungen, die lang-, mittel- und kurzwellig sind.

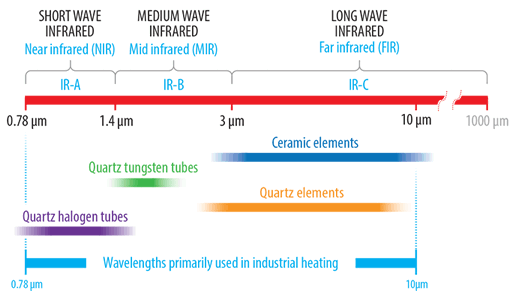
Langwellenemitter, auch als Ferninfrarot (FIR) bekannt, haben einen Spitzenemissionsbereich im 3-10 μm-Bereich. Dieser Bereich bezieht sich allgemein auf keramische Elemente, die aus einer hochtemperaturbeständigen Legierungsspule bestehen, die entweder in einen massiven oder in einen hohlen, hochemittierenden Keramikkörper eingebettet ist. Keramikstrahler werden in einer Reihe von Industriestandardgrößen mit entweder flachen oder gekrümmten (rinnenartigen) emittierenden Oberflächen hergestellt.

Kürzere Spitzenemissionswellenlängen werden durch Verwendung von Emissionsquellen mit höheren Oberflächentemperaturen erreicht. Quarzkassetten-Strahler sind in ähnlichen Industriestandardgrößen wie Keramik erhältlich und bestehen aus einer Reihe durchscheinender Quarzröhren, die in ein poliertes aluminisiertes Stahlgehäuse eingebaut sind. Diese Strahler können mit einer höheren Vorderflächentemperatur arbeiten und im lang- bis mittelwelligen Bereich emittieren.

Am kürzeren Ende des Mittelwellenbereichs befindet sich der Quarz-Wolfram-Emitter, der aus einer versiegelten linearen klaren Quarzröhre mit einer Wolframspule in Sternform besteht. Die Wolframspule bietet eine schnelle Reaktionszeit bei geringer thermischer Trägheit.

Der kurzwellige Quarzhalogenbereich ist ähnlich aufgebaut wie der des schnellen mittelwelligen Wolframstrahlers mit der Ausnahme, dass eine runde Wolframspule verwendet wird und Quarzrohre mit Halogengas gefüllt sind. Die höhere Spulentemperatur führt zur Erzeugung von weißem Licht und einer Spitzenemissionswellenlänge im Kurzwellenbereich.

Erläuterungen zum Planckschen Gesetz

Das Plancksche Gesetz besagt, dass mit steigender Temperatur einer emittierenden Oberfläche immer mehr Energie als Infrarotenergie freigesetzt wird. Je höher die Objekttemperatur ist, desto mehr Infrarotenergie wird erzeugt. Die emittierten Frequenzen werden nicht nur intensiver (Leistung), sondern auch breiter und die Spitzenwellenlänge kürzer.

Bei sehr hohen Temperaturen, nicht nur im Infrarotbereich, wird auch sichtbares Licht mit kürzerer Wellenlänge erzeugt. Dies wird zuerst als ein mattes rotes Leuchten, dann als Orange, Gelb und schließlich als Weiß beobachtet. Abbildung 1 (unten) zeigt typische Plancksche Gesetzkurven für einen Temperaturbereich von 1050 ° C bis 50 ° C.

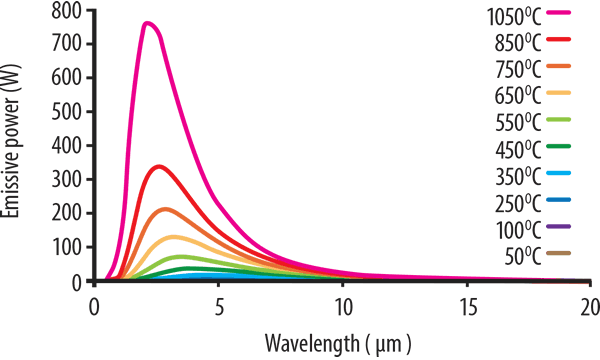
Die rosa Kurve, die 1050 ° C entspricht, zeigt die stärkste Ausgabe. Es zeigt die höchste Ausgangsleistung und seine Spitze liegt bei etwa 2.5 Mikrometer. Daran schließt sich die Kurve bei 850 ° C an, bei der die Spitzenenergie weniger als die Hälfte der bei 1150 ° C erzeugten Energie beträgt.

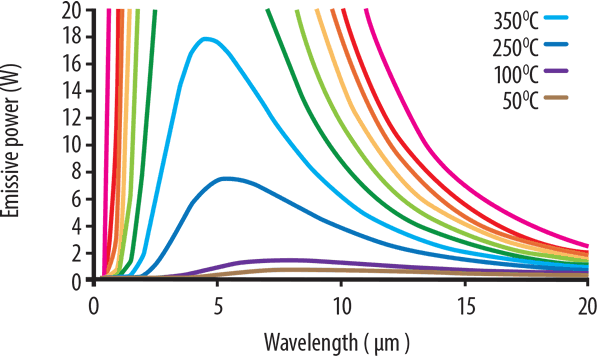
Mit abnehmender Temperatur sinken auch die Energieniveaus und die Wellenlänge der Spitzenenergie verschiebt sich zu den längeren Wellenlängen. Die niedrigsten Temperaturen aus den 250 ° C-, 100 ° C- und 50 ° C-Kurven sind in der Grafik nicht zu sehen. Wenn die Grafik jedoch vergrößert wird, um die niedrigeren Temperaturkurven zu sehen, ist diese Verschiebung zu den längeren Wellenlängen deutlicher. Die Leistungsintensität nimmt jedoch deutlich ab.

Dies ist in Abbildung 2 (unten) dargestellt. Bei 250 ° C weist die blaue Kurve einen ungefähren Peak von ~ 6 Mikrometer auf, während bei 100 ° C die Peakwellenlänge ~ 7.5 Mikrometer beträgt. Es ist auch zu beachten, dass das Ausmaß der Wellenlänge gleichmäßiger verteilt ist und nicht den konzentrierten schmalen Peak zeigt, der bei höheren Temperaturen zu sehen ist.

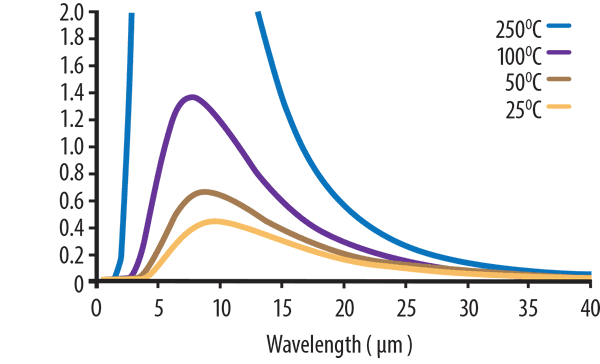
Wenn wir den gleichen Graphen erneut vergrößern und uns nur auf die niedrigeren Temperaturen konzentrieren, wie in Abbildung 3 (unten) gezeigt, sehen wir, dass die Temperaturen von 50 ° C und 25 ° C Spitzenwellenlängen von ~ 9 bzw. 10 Mikrometer haben.

Anwenden dieser Informationen

Als Experten auf unserem Gebiet hoffen wir, dass diese Informationsseiten Ihnen helfen, Infrarot besser zu verstehen. Das Wichtigste ist zu wissen, was Ihr Material ist und wofür Sie Ihr Material benötigen. Wir können Sie im Rest beraten!