The application of infrared heat in industrial processes
The following page links offer a comprehensive overview of how to apply infrared heat precisely and efficiently, to heat products and components in an industrial process.
- About infrared (IR) heat
- Types of heat transfer
- Application of infrared heat to materials
- The fundamental laws of infrared heating
Principles, Definitions, and Laws
Infrared (IR) heating is an exact and measurable science. With its own history and terminology, it’s framed and bound by several perpetual scientific and physical laws. While we consider these principles and laws, we also outline the main applications for IR heating technology as it’s practised today.
At its most basic, IR heat is produced through temperature differentials between objects. Any object at a temperature greater than 0 K (-273.15°C) radiates infrared energy, and when one object is hotter than another, IR energy will flow from the hotter object to the colder one. The surface of the objects will play a key role in both the emission of the IR energy and in the absorption of the energy emitted.
Where infrared appears on the electromagnetic spectrum
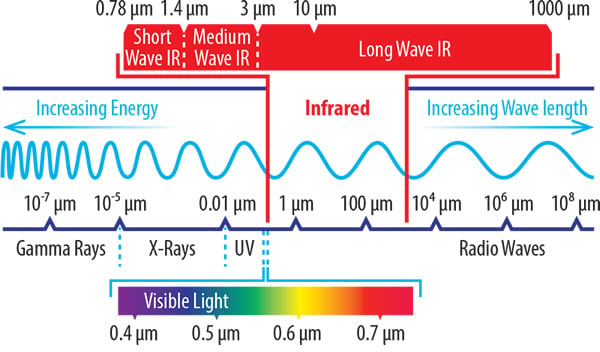
Sharing several characteristics of solar radiation, it’s sometimes popularly described as ‘sunshine without light’. The physics of IR energy are similar to light – another solar property. However, most of the IR spectrum lies beyond that which is visible to the human eye. As such, infrared heat can be best thought of as a form of energy or radiation.
But in scientific terms, IR heat is a wave of electromagnetic radiation. And for industrial purposes, these IR waves are utilised in three main forms of delivery:
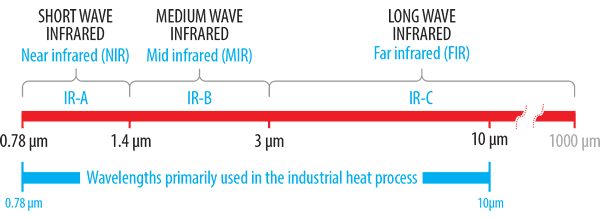
Shortwave (0.78 – 1.4 μm)
Mediumwave (1.4 – 3 μm)
Longwave (3 – 1000 μm)
The key principles of heating and heat transfer – non-IR based
Heat is defined as energy transferred by virtue of a temperature difference. As heat only moves in one direction, flowing from regions of higher temperature to regions of lower temperature, heat energy will naturally flow from one to the other until both regions are the same temperature.
Definitions used in the measurement of heat
 Heat is a form of energy and is measured in either Joules (J) or British Thermal Units (BTUs). The Joule is an SI unit and is most commonly used in this sector. BTUs is a mainly US term despite its name. The calorie (cal) is rarely used in the IR sector.
Heat is a form of energy and is measured in either Joules (J) or British Thermal Units (BTUs). The Joule is an SI unit and is most commonly used in this sector. BTUs is a mainly US term despite its name. The calorie (cal) is rarely used in the IR sector.
Heating power is measured in Watts (W) and is defined as one Joule per second.
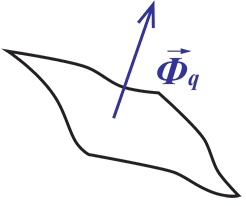
Heat Flux (Φq) is defined as heating power per unit area and is measured in units – either W/m2 or W/cm2.
Definitions used in the measurement of temperature
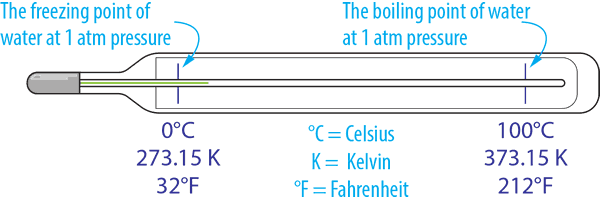
With temperature measured using several scales the most commonly used in the industry is Degrees Celsius (°C). However, Kelvin (K) is a more scientific unit that has an absolute scale, while Fahrenheit (°F) is used mainly in the USA.
Next page: Types of heat transfer